What do we mean by the term “Regression”?

Let’s understand this concept with a simple example. You want to apply for US University to pursue a Master’s degree. Then the factors on which whether you will get an admission letter from a particular University depends on the following factors i.e. GRE Score, TOEFL Score, Number of research papers published, SOP and Letter of recommendation so, basically speaking in data science terms these are your independent variables and the chances of you being admitted into a university is your dependent variable which you predict based on your independent variables. In simple terms, the thing which you need to predict falls under the dependent variable and the factors on which your prediction is based are your independent variables.

So, when you want to plot the relation between your dependent and independent variable you need to perform regression analysis. Most importantly your dependent variable MUST be a numeric value. The relationship between dependent and independent variables in the case of linear regression is of linear nature.

The meaning of the term “Linear” is whenever the independent variable(X) increases the dependent variable (Y) also increases.

Types of Linear Regressions

The count of independent variables is not always the same, some times there can be one independent variable or multiple independent variables.

So, whenever there is only one independent variable we call it Simple Linear Regression and when there are more than one independent variables we call it Multiple Linear Regression.

Simple Linear Regression

Simple linear regression can be simply represented by the following equation. You can also compare this with the equation of a straight line y=mx+c.

Multiple Linear Regression

When there are multiple independent variables we use the following equation. There can be a’n’ number of independent variables.

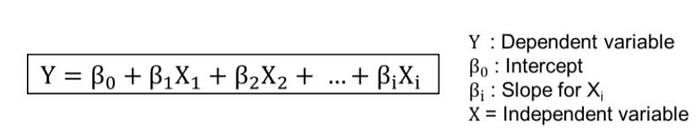
Regression Coefficient(β)

Now, let’s understand the importance of the regression coefficient (β). In simpler terms ‘β’ helps the model to decide which independent variable will have the most impact on your dependent variable. The greater the value of ‘β’ more is its importance in the model.

In this example, we can see that the independent variable ‘x3’ has the maximum value (i.e. Regression Coefficient(β) is maximum). This shows that ‘x3’ is an important feature in predicting the dependent variable ‘Y’.

Y = 1 x1 + 0.5 x2 + 5 x3 + 0.3 x4

If you enjoyed this article, share it with your friends and colleagues!